Excel雷达图绘制极坐标阿基米德螺线方程曲线

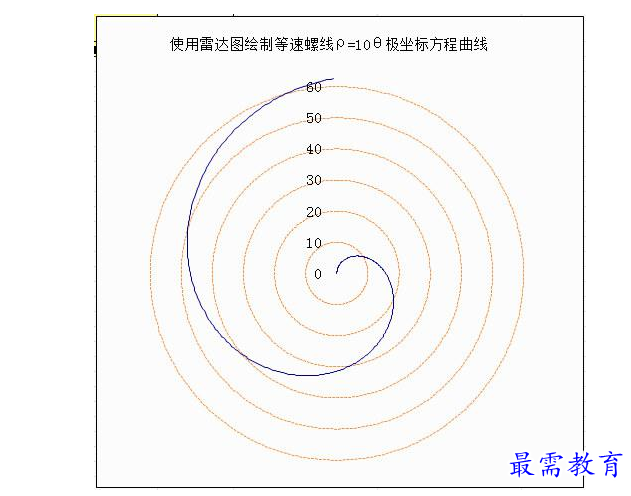
  本文讲述内容并非是Excel雷达图设计时的本来用途，而是突发奇想，发现用它来绘制极坐标既符合极坐标的思想方法，方法又极其简单，尤其是二次曲线和一些特殊的螺线。与思想方法相比，初相和旋转方向的差异几乎可以不必顾及，因为那是很容易理解并有简单的数学方法来解决的。

      Excel中的雷达图与解析几何中的极坐标既相似又相异。

      主要的相似处就是：它们都是从一个中心点沿着射线方向出发，使用离开中心的径向距离，作为定位参数中的一个指标。

      主要的相异处（另一相异处将在后面单独列出）就是：

      极坐标是以向右方向（正东，方位角90°）为起始位置，以逆时针方向角度为正值，且往往以弧度计值，从而作为定位参数的另一个指标。极坐标的极角是任意角，可正可负，可大于一个圆周角、多个圆周角乃至于N个圆周角周而复始地旋转；

      而雷达图没有角的概念，它是以参与作图的数据点个数来平分中心角，各个数据点按相同的角增量，再按上述第一个径向距离定位。如果使雷达图模拟一个圆周角，就要设置360个数据点。不必多于360，因为即使设置720、1080个数据点，它也是将一个周角等分成720份、1080份来处理。

      基于上述分析，可以用Excel雷达图模拟极坐标来绘制一些极坐标方程的曲线，因为不需要将极坐标方程各点坐标转换成直角坐标后，再在直角坐标系绘制散点图，可以在雷达图直接绘制。不过要注意几点：数据点最好取360个（0～259）；每个角度要化成弧度：1°≈0.017（弧度）

      对于三角函数，如是以2π为周期的，在极坐标方程中表现为闭合0～2π之间的心脏线，如周期有所变化的，在0～2π之间的表现周而复始的多叶线；对于发散性的螺线，就要注意起始和终结处的处理。

      先作准备工作：在M2单元格设定1°的角对应的弧度，对M2使用绝对引用。

      A列从A3开始为X在[0,359]上取值，从0开始，到359，数据间隔为1;

      B列从B3开始是公式，将角度换算成弧度：在B3中键入=A3*$M$2，对M2单元格中1°的角对应的弧度数的值使用绝对引用，对A3单元格的角度的值使用相对引用。然后向下拖曳复制到与A列相对应的B362：

      先以三角函数的心脏线为例。

      ρ=sinθ

      在C3中键入=SIN(B3)，对B3单元格中已换算好的θ取值的弧度数使用相对引用。然后向下拖曳复制到与A列相对应的C362。

      只需选取C3：C362，选作雷达图即可。删去图例、数据标志等，就可得下图。这也是条封闭的曲线，与极坐标系做的同一曲线图差了90°这是起始位置相异所致。另外在图中也可以看到雷达图对于负值的处理：